Matek-Wigyorival
- Elmélet egyszerűen
- Számoljunk! - 6.

A vadász találkozik a keservesen zokogó Piroskával az erdőben. Megkérdi tőle:
- Miért sírsz ennyire, Piroska?
- Mert háromszor is megerőszakolt az a csúnya, gonosz farkas!
- Mikor történt ez??.
- Tegnapelőtt... meg tegnap... meg ma is oda megyek...

Elérkeztünk a számolással a "6"-os számhoz. Ehhez, ha az ujjainkon számolunk, kevés kivételtől eltekintve, már szükségünk lesz mindkét kezünkre. Számelméleti szempontból a "6" az első összetett, nem négyzetszám, azaz két (vagy több) különböző prímszám szorzata.
A "6"-os szám ugyanakkor 3+3, azaz két Mesterszám együtt. A "3"-ast ugye egy forgó Jin-yang szimbólumhoz hasonlítottuk. A két, önmagában működő rendszer (a két "3"-as) vagy segítik egymás munkáját vagy rontják egymás teljesítményét.
A geometriában is fontos szerepet tölt be ez a szám. A 3 dimenzióban, azaz a térben az alap sokszögű test a kocka, amelyet 6 egyforma négyzet határol. A játékokból jól ismert alap dobókockáknak is 6 oldala van, a 6 pötty jelzi a legnagyobb dobást.
Az ezoteriában a 6-os szám az emberrel függ össze. A Biblia szerint a 6. nap teremtette Isten az első embert, Ádámot. Akinek utódai az Édenkertből való kiűzetés óta a Tudást keresik, amivel újra hatalmuk lehet magán az Időn. A 6-os szám akkor jelent igazi gonoszságot, amikor háromszor is le van írva egymás után. Mint tudjuk, a 666 az antikisztus és a sátán száma. Ennél kissé szolídabb a helyzet, ha csak kétszer írjuk le. A 66-ról egyrészt eszünkbe juthat az USÁ-t átszelő legendás autóút. Másrészt a szintén legendás 66-os parancs, ami miatt a klónsereg lemészárolta a jediket a Sithek bosszújában.
Ahogy már írtam, a 6-os tulajdonképpen két 3-as. Épp ezért, vizsgáljuk meg most alaposabban a geometria egyik alappillérét, az első sokszöget: a háromszöget.
A síkban minden sokszög felbontható háromszögekre, ehhez csak annyi kell, hogy egy adott csúcsból meghúzzuk az összes átlót. Minden sokszögre igaz, hogy egy adott csúcsból pont 3-mal kevesebb átlót tudunk húzni, mint ahány csúcsa van a sokszögnek, mivel önmagába és a két szomszédos csúcsba nem tudunk átlót húzni. Tehát, n oldalú sokszögnél egy csúcsból n-3 átlót tudunk húzni. Ugyanakkor a síkidom összes meghúzható átlóját úgy tudjuk kiszámolni, hogy az egy csúcsból húzható átlók számát megszorozzuk a csúcsok számával, aztán elosztjuk 2-vel, merthogy minden átló 2-2 csúcsot köt össze, tehát oda-vissza érvényes.
Ha egy csúcsból meghúzzuk az összes átlót, a sokszöget pont 2-vel kevesebb háromszögre bontjuk fel, mint ahány oldala van a sokszögnek.
A háromszögeknél nagyon fontos, hogy ha összeadjuk a szögeket, pont 180 fokot kapunk. Épp ezért minden sokszög belső szögeinek összege az oldalak számánál 2-vel kevesebbszer 180 fok, azaz (n-2)*180°.
Még két nagyon fontos szabály vonatkozik a háromszögekre, mégpedig az, hogy bármely két oldal összege nagyobb, mint a harmadik oldal, valamint nagyobb oldallal szemközt nagyobb szög is van, egyforma oldalakkal szemben pedig egyenlők a szögek is.
A háromszögeket megkülönböztethetjük szögeik alalpján. A hegyesszögű háromszögnek mind a 3 szöge hegyesszög, a derékszögűnek van 1 derékszöge, a tompaszögűnek pedig 1 tompaszöge. 2 derékszög vagy tompaszög azért nem lehet egy háromszögön belül, mert 2 derékszög már összesen 180°, tehát nem marad semmi a harmadikhoz (2 tompaszög pedig több is).
Az oldalak hossza alapján is lesznek speciális háromszögek. Ha 2 oldal egyforma hosszú, egyenlő szárú háromszögnek nevezzük, ha mind a 3 egyforma, akkor egyenlő oldalú vagy szabályos háromszögnek hívjuk. (A szabályos síkidom azt jelenti, hogy a sokszög összes oldala és összes szöge egyforma nagyságú.)
A háromszögeknél több különleges egyenesről és pontról kell említést tennünk.
1. Oldalfelező merőleges. Mint a neve is mutatja, az oldalak felezőpontjára húzunk egy-egy merőlegest. A három oldalfelező merőleges egy pontban metszi egymást: ez a háromszög köréírható körének a középpontja.
2. Szögfelező egyenes. A csúcsokból húzott egyenesek, amik felezik azt a szöget, ahonnan kiindulnak. A három szögfelező egy pontban metszi egymást: ez a háromszög beírható körének középpontja.
3. Magasságvonal. Egy csúcsból merőlegest bocsátunk a szemközti oldalra. A három magasságvonal egy pontban metszi egymást: ez a háromszög magasságpontja.
4. Súlyvonal. Egy csúcsot és a szemközti oldal felezőpontját összekötő egyenes. A három súlyvonal egy pontban metszi egymást: ez a háromszög súlypontja.
5. Felezővonal. Két-két oldal felezőpontját összkötő egyenes. A három felezővonal a háromszöget 4 kisebb háromszögre bontja, melyek egymáshoz is és az eredeti háromszöghöz is hasonlóak.
A szabályos háromszögben a köré- és beírható kör középpontja, valamint a súlypont és a magasságpont egy helyre esik. Ennek ábrázolása kiváló kiindulópont "okkultista" szimbólumok megrajzolásához:

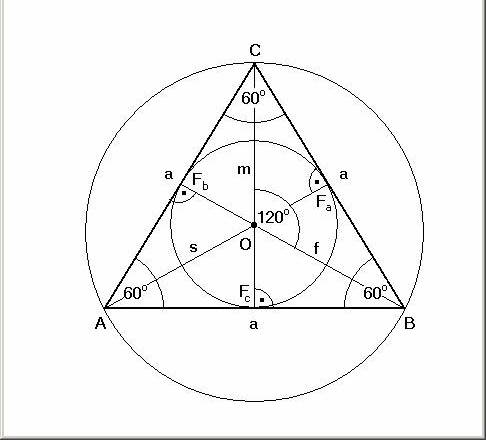
Említettem már, hogy a sík bármely pontját meghatározhatjuk két, egymásra merőleges számegyenes segítségével (koordináta-rendszer). Pont a merőlegesség miatt kiemelten fontosak a derékszögű háromszögek.
A derékszögű háromszögeknél több érdekes szabályosságot is találunk. Az egyik nagyon fontos tulajdonság, hogy a derékszögű háromszög befogóinak (rövidebb oldalak) négyzetének összege megegyezik az átfogó (azaz a leghosszabb oldal) négyzetével. Ezt mevezzük Pitagorasz-tételnek, amit képlettel így írunk le: a²+b²=c²
Tehát ezeknél a háromszögeknél 2 oldal hosszának ismeretében könnyen kiszámolhatjuk a harmadik oldalt.
Másik érdekes szabály, hogy a derékszögű háromszög köréirható körének középpontja mindig az átfogó felezőpontjára esik, és a kör sugarának hossza megegyezik az átfogó felével. Ez a Thales-tétel. Ebből persze az is következik, hogy ha egy szakasz felezőpontjából húzunk egy a szakasz felével megegyező sugarú körívet, akkor a körív minden pontján az adott szakasz derékszögben látszik.
A derékszögű háromszög oldalai és szögei között további összefüggéseket is megfigyeltek. Ezekkel a trigonometriai szabályokkal, egy-egy adott hegyesszög szinuszát, koszinuszát és tangensét tudjuk kiszámolni. A szinuszt a szög melletti befogó és az átfogó, a koszinuszt a szöggel szemközti befogó és az átfogó, a tangenst pedig a szög melletti és a szöggel szemközti befogó hányadosaként kapjuk meg. Tehát:

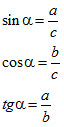
A szögfüggvényeket az általános háromszögekre is tudjuk alkalmazni. A szinusztétel kimondja, hogy a háromszög egy-egy oldalának és a vele szemközti szög szinuszának aránya a háromszögön belül megegyezik. Tehát:

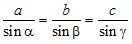
A koszinusztétellel pedig két oldal és az általuk közrezárt szög alapján ki tudjuk számolni a harmadik oldalt:

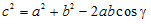
Ezek a szabályok rendkívül fontosak az elemi síkgeometriában. A következő fejezetben ismét visszatérünk az algebrához. Addig is emésztgessétek a tanultakat!
Továbblépés a "7"-re